Audio Deep Learning- 푸리에 변환
Audio Deep Learning - 푸리에 변환
소리란?
진동으로 인한 공기의 압축이다.
소리에서 얻을 수 있는 물리량
- Amplitude : 진폭
- Frequency : 주파수
- Phase : 위상
물리 음향의 경우 진폭의 세기, 소리 떨림의 바르기, 소리파동의 모양으로 각각 매핑되며
심리 음향의 경우 소리의 크기, 음정,소리의 높낮이/진동수, 음색:소리 감각이 매핑된다.
Frequency 의 경우 Hertz를 사용하며, 주파기는 sin 주기 $2\pi /w$ 로 나타난다.
Complex Wave : 우리가 사용하는 대부분의 소리들은 복합파이다. 복합파는 복수의 서로 다른 정형파들의 합으로 이루어진 파형(Wave)이다. 소리는 여러 주파수의 Sumation 으로 이루어진 것이다.
정현파 ? 일종의 복소주기함수
- 0-1. Sound Classification & Auto - tagging

해당 작업은 소리의 파형을 인풋으로 받아 Output으로 해당 소리의 출처를 Tagging 하거나 소리의 파형에 태깅을 하는 작업이 있다.
- Speech To Text(STT) : 음성을 텍스트로 변환하는 작업을 나타낸다. 음성 인식 기술로써 ASR 이라고 부르기도 하는데 , LAS , CPC, Word2Vec과 같은 논문들이 해당 Task 틑 통한 것이라고 할 수 있다. 현재 STT의 정확도는 상당히 높은 편이다.
- Text To Speech(TTS) : 텍스트를 입력받아 사람의 음성처럼 합성해주는 Task 이다. 주로 Text -> Spectogram -> Speech 형태로 합성이 이루어진다.
Digital Signal
오일러 공식
임의의 복소수 $x+iy$ 에서, $x,y$ 는 실수라고 하고 극 좌표계로 표현하기 위해 $r$ 이 $x,y$까지의 거리고 $x$축과 이루는 각도가 $\theta$라고 할 때
$x+iy = rcos(\theta) + ir~sin(\theta)$
$r=1$인 경우를 $z$라고할 때
$z = cos(\theta) + isin(\theta)$ 가 되며 $z$ 라는 값은 반지름 1인 단위 원 상의 점이 된다.
여기서 $z$ 를 $\theta$에 대해 미분한다면
$\frac{dz}{d\theta} = -sin(\theta) + icos(\theta)$ 이고 해당 식 양변에 $-i$를 곱해주게 되면
$-i\frac{dz}{d\theta} = cos(\theta) + isin(\theta)$
위 식은 $z$와 같으므로 $ z= i\frac{dz}{d\theta}$ 이고 해당 식을 변형하게 된다면
$\frac{dz}{z} = id\theta$ 이고 양변을 적분하면
$ln(z) = i\theta + C$ 이다. 위 식을 다시 쓰면
$z = Ae^{i\theta}$ 이고
$cos(\theta) + isin(\theta)= Ae^{i\theta}$ 이며 $\theta = 0$을 대입하면 $A$는 1 이 된다.
따라서 $e^{i\theta} = \cos(\theta) + i\sin(\theta)$ 가 된다.
즉, 오일러 공식의 경우 허수가 포함된 식을 극 좌표계로 표현할 때 유도되는 식이라고 할 수 있으며, $r=1$ 인 단위원 상황에서 나타나는 식이다.
위 오일러 공식의 우변 $\cos(\theta) + i\sin(\theta)$의 경우 그냥 풀어쓰면 $x+iy$ 가 되므로 어떠한 복소수 값이라고 할 수 있는데, 극 좌표계에서의 표현은 단위원 안에서 나타낼 수 있다.
따라서 해당 공식에서의 $e^{i\theta}$ 는 복소수이지만, 단위원 내의 $\theta$의 각을 갖는 호의 점이라고 판단할 수 있다.
소리의 물리량
소리란 진동으로 인한 공기의 압축으로 생성되는데, 진폭(Amplitude), 주파수(Frequency) , 위상(Phase)란 세가지 물리량에 주로 의존한다.
- Amplitude : 파장의 크기로 파장의 높이
- Frequency : 파장의 간격으로 삼각함수의 주기의 역수
- Phase : 파장의 고유한 모양으로 쇳소리, 물소리 음과 세기가 달라도 주기의 모형이 다를 수 있다.
Sinusoid
정현파(Sinusoid)는 주기신호를 총칭하는 말이다.
정현파의 본질은 원 위의 회전과 관련된 것이다. 또한 시간에 따른 회전을 이야기하는 것이다.
4초 주기로 원 위의 점이 회전하고 있다. (출처 : https://angeloyeo.github.io/2022/01/04/sinusoids.html)
해당 원에서 우리는 빨간 점의 2차원 상의 위치 정보를 표현하기 위해 어떠한 작업을 거쳐야 하는가?
그림. 4초 주기로 원 위의 점의 x 축 y 축 위의 변화만을 관찰하는 과정
그림 . 원 위의 회전에 맞춰 x 축 y 축의 시간 변화를 각각 그래프로 표현하면 정현파를 얻을 수 있다.
원의 회전에서 $x$축, $y$축의 움직임은 단순히 $cos,sin$함수에 해당한다.
즉, 삼각함수는 원을 회전하는 점의 Vector Space 안에서의 위치 정보를 담는 함수라고 생각할 수 있다.
또한 정현파는 이렇듯 원의 회전에서 부터 생각이 가능한데,
$[x(t)=A\cos(2\pi f_0 t+\phi) = A\cos(\omega_0 t + \phi)]$ 라고 정현파를 표현할 수 있다. 여기서 $A$ 는 진폭(Amplitude)인데, 여기 표현에서는 상수 취급을 한다. 이 진폭을 원의 회전 의미로 나타내면, $r=A$ 인 반지름을 가진 원을 회전하는 것이라고 나타낼 수 있다.
$\omega_0$는 주파($2\pi f$)로 표현할 수 있는데, 삼각함수는 한번 회전할 때 $2\pi$라는 각도를 회전한다. $\omega_0$ 는 이 회전 수의 역수를 나타낸 것이라고 할 수 있으며 보통 HZ(헤르츠)로 표현한다. 보통 440Hz 는 1번 회전 시 1/440초 안에 회전을 한다는 뜻이다. (주기의 역수)
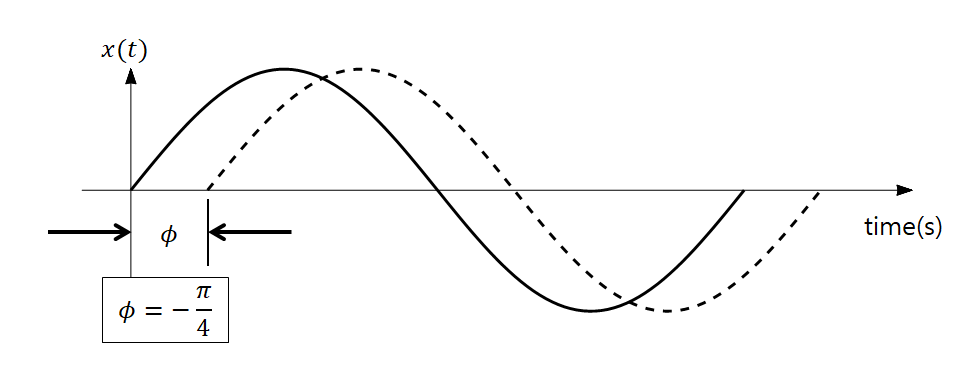
또한 $\Phi$는 각 소리의 위상이라고 할 수 있으며 해당 삼각함수에서 x축의 shift 한 형태꼴로 나타난다. 다시 말해 위상만 다른 두 삼각함수는 시작 위치만 다른 것이다.
Sampling
소리는 시간에 따른 연속적인 데이터이다. 하지만 이러한 데이터를 컴퓨터에 집어넣기위해 양자화를 통해 이산화 작업을 거쳐야 한다.
우선 먼저 시간의 범위와 단위 시간에 들어가는 양을 정의해야하는데, 이 작업을 Sampling 이라고 한다.
1초의 신호를 몇개의 숫자들의 Sequence로 표현하는가를 Sampling rate $f_s$라고 한다.
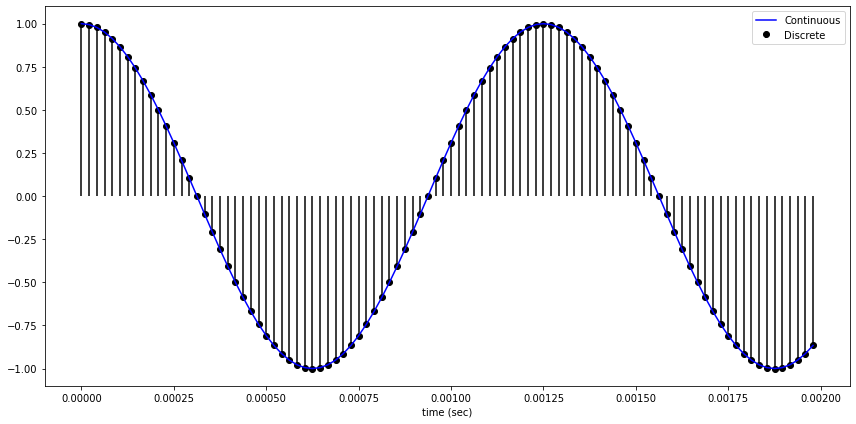
$x_s[n] = x_c(nT_s) = x_c(\frac{n}{f_x}))$
위 식으로 표현이 가능한데, 해당 식에서 $[n]$ 이란, 보통 이산화를 시켜 함수 값을 표현하기 때문에 표기 상 나타낸 것이고 $nT_s$ 란, $T_s$라는 시간 구간 안에서 n 번 째 값인 것이다.
여기서 sr이 매우 커지게 된다면, 기본 데이터를 잘 복원할 수 있을 것이다.
예를 들어 $f_s$ 가 20000이라면 1초의 주기에서 총 2만개의 데이터 Sequence를 추출하겠다는 의미이다.
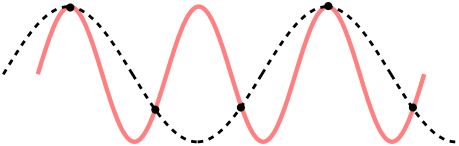
만약 Sampling이 생각보다 크다면 즉, Sampling 의 크기가 파장의 최대 주파수(가장 작은 주기)보다 크다고 가정한다면, Sampling 되는 포인트가 한 주기를 넘어갈 수 있기 때문에 Sampling 을 하는 것이 파장의 모양을 적절하게 반영하지 못할 수 있다.
따라서 파장의 모양에 따라 Sampling rate를 조정하여 적절하게 Sampling 을 해야하는데, Nyquist 이론에 의해 Sampling rate 가 원래 신호에 존재하는 주파수의 최댓값2배보다 크면 원래 신호를 손실없이 복원할 수 있다.
즉, $f_m < f_s$ 에서 $f_m$은 최대 주파수를 의미한다. 일반적으로 Audio CD의 경우 44.1kHz, Speech는 8kHz의 sampling rate 를 사용한다.
Quantization
Quantization 은 초당 sr만큼 Sampling 데이터가 있을 때 해당 구간에서 Amplitude 를 반홀림하여 Bit로 나타낸다. 즉, 주기 그래프에서 수직선이 Sampling 된 값이라면 수평선이 Quantization 된 값이다.
해당 작업을 진행하는 이유는, Amplitude 즉, 진폭은 자연에서 연속형 수치이기 때문에 컴퓨터에 저장하기 위해 이산화 작업을 거쳐야하기 때문이다.
보통 N bit 의 Quantization 의 경우 $-2^{N-1}$ ~ $2^{N-1}-1$ 사이의 Bit 로 나타내며, 16Bit 의 경우 N 에 16을 대입한 구간에서의 Bit 로 나타낸다.
해당 구간의 의미는 이산화 작업 시 N 비트에서 연속형 값이 매핑될 수 있는 구간을 의미한다.
Quantization 을 하기 위해 각 스탭마다의 값을 추출하기 위해 $\Lambda = \vert t-s\vert / (\lambda -1)$ 라는 범위 값을 사용한다. 예를 들어 $\Lambda = 0.25$ 라면, Amplitude 가 1 과 2사이인 구간을 4등분 한 후 마루/천장 함수를 거치기 때문에 오차는 최대 $0.125\Lambda$가 될 것이다. (ex : $1.375\Lambda \sim 1.25\Lambda$,$ 1.376\Lambda \sim 1.5\Lambda$)
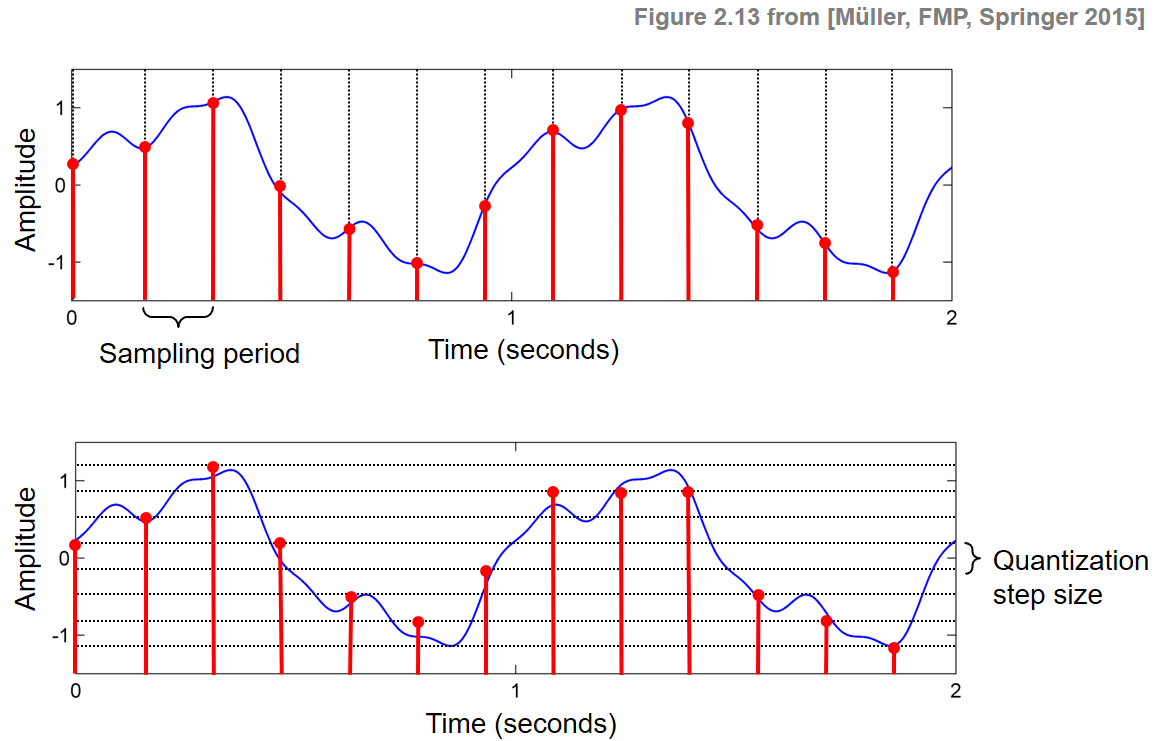
해당 그림에서 Quatization Step size 가 $\Lambda$ 라고 할 수 있다.
우선 -1~1 영역으로 Scailing 을 하여 Quantization 을 진행하는데, 그 이유는 Quantization 발생 시 필연적으로 생기는 Error Loss 를 줄이기 위함이다.
이렇게 Quantization을 진행할 경우 음질은 떨어지지만 Light한 자료형을 얻을 수 있다.
Fourier Series
푸리에 변환이란, 임의의 입력신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현하는 것이다.
앞서 정현파는 주기함수의 집합이라고 나타내었는데, 해당 의미는 원 위의 점을 시간에 따라 표현하는 것이라고 할 수 있다.
하지만 점이 회전할 때 어떠한 패턴을 갖고있기는 하지만 도무지 파악할 수 없는 패턴으로 나타날 때, 종합된 패턴을 여러 성분 패턴으로 분해하여 하나씩 파악하는 것이 푸리에 급수(변환)이라고 할 수 있다.
예를 들어 결과물 스파게티를 보고 어떤 재료가 얼마나 들어갔는지 펼쳐 보여주는 것이라고 할 수 있다.
푸리에 분석의 과정은 여러 정현파 후보들을 가져온 후 시퀀스 당 내적을 통해 닮음 정도를 검사하는 것이라고 할 수 있다.
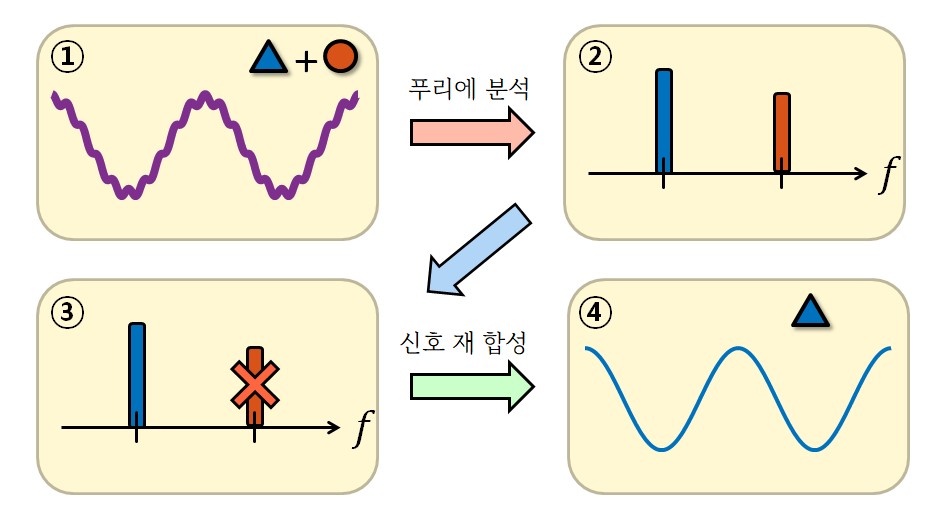
해당 푸리에 변환 과정은 어찌보면 Attention 메커니즘과 비슷하다고 할 수 있다.
Attention 의 경우 합성된 결과를 토대로 여러 이전 정보들의 강도 $c$를 구해 해당 세기 또한 학습하는 것이라면 푸리에 변환 과정에서는 합성된 결과를 토대로 단순히 신호의 이전 형태를 나타내는 것이다.
어떤 시간 $t$ 시점의 합성된 신호 $x(t)$는 Vector Space 상에 존재하기 때문에 기저 신호 벡터 {$\psi_i(t)$}의 집합으로 표현할 수 있다.
$x(t) = \sum_i c_i \psi_i(t)$
우리는 이 $\psi$ 만 구할 수 있다면 아래와 같이 $c_i$만 구하게 되면 $x(t)$를 표현할 수 있다. 아래 그림과 같이 기저 신호의 성분량 $c$만을 이용해 원 신호를 표현해주는 방법을 스펙트럼 분해라고 한다.
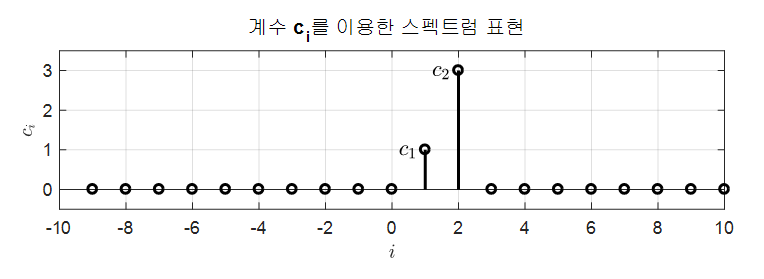
따라서 적절한 신호 후보군들을 찾는 것이 중요하다고 할 수 있는데, 선행 연구들에서 제시하는 가이드 라인을 통해 보통 복소 정현파(삼각함수)를 기저함수(후보군)로 갖게 된다.
여기서 복소 정현파를 사용하는 이유는 신호를 시스템으로 변환할 때 계산 편의성을 위함이다.
또한 푸리에 결과에 따르면 주기 신호는 같은 주기를 갖는 정현파와 이 정현파의 정수배를 갖는 정현파의 합으로 표현할 수 있기 때문에 아래 식과 같이 정현파의 선형결합으로 표현할 수 있다.
$x(t)=a_0+\sum_{k=1}^\infty a_k\cos\left(\frac{2\pi k t}{T}\right)+\sum_{k=1}^{\infty} b_k \sin\left(\frac{2\pi k t}{T}\right)$
위 식에서 각 정현파를 복소 정현파라고 했기 때문에 오일러 공식을 적용하여 하나의 Summation 으로 묶을 수 있다.
$x(t)=a_0+\sum_{k=1}^\infty a_k \cos(\frac{2 \pi k t}{T})+\sum_{k=1}^{\infty} b_k \sin (\frac{2\pi k t}{T})$
$=a_0+\sum_{k=1}^{\infty}(a_k\frac{\exp\left(j 2\pi k t/T\right)+\exp\left(-j2\pi k t/T\right)}{2} + b_k\frac{\exp\left(j 2\pi k t/T\right)-\exp\left(-j 2\pi k t/T\right)}{2j})$
$=a_0+\sum_{k=1}^{\infty}\left(\frac{a_k-jb_k}{2}\exp\left(j\frac{2\pi k t}{T}\right)+\frac{a_k+jb_k}{2}\exp\left(-j\frac{2\pi kt}{T}\right)\right)$
$=\sum_{k=-\infty}^{\infty}c_k\exp\left(j\frac{2\pi k t}{T}\right)$
여기서 $c_k$는 $a_0, a_k, b_k$와 다음과 같은 관계를 갖는다고 볼 수 있다.
$ c_k = \begin{cases} \frac{1}{2} (a_k-jb_k), && k >0 \ a_0, && k = 0 \ \frac{1}{2} (a_k+jb_k), && k < 0 \end{cases} $
결론적으로 우리는 복소 삼각함수를 이용해 임의의 연속 신호 $x(t)$를 표현할 수 있다.
위 식에서 신호 $x(t)$를 표현한 것이 복소 평면 내에 자연상수로 표현했는데, 오일러 공식을 통해 유도하였다.
위 결과가 제시하는 바는 해당 시점 $t$에서 단위원 위의 각기 다른 주기를 갖는 점들의 선형 결합으로 $x(t)$ 에서의 점을 표현할 수 있다는 것이다.
위 식에서 $k =i$일 때 각 점들에 대해 판단하게 된다면 각$\exp\left(j\frac{2\pi k t}{T}\right)$ 를 기저함수로 하여 실제 점 $x(t)$를 표현하는 것이다. ( $T$ 가 주기)
\[c_k = \frac{1}{T}\int_{0}^{T}x(t)\exp\left(-j\frac{2\pi k t}{T}\right)dt\]해당 Flow 를 다시 표현하자면
- 어떤 정현파는 다른 정현파들 성분들의 합으로 나타낼 수 있다.
- 따라서 $x(t) = \sum_i c_i \psi_i(t)$ 로 나타내었다.
- 후보군$\psi$를 정하기 위해 복소 정현파(복소 삼각함수)를 사용하였다.(편의를 위해)
- 복소 삼각함수에서 오일러 공식을 적용하기 위해 $x(t)$ 를 같은 주기를 갖는 정현파의 정수배 꼴로 나타냈다.
- 오일러 공식을 적용하여 $\exp\left(j\frac{2\pi k t}{T}\right)$ 를 기저로 하는 선형 결합 꼴로 $x(t)$를 나타내었다.
Fourier Transformation
푸리에 변환의 아이디어는 $T$를 주기로 하는 주기함수 $x(t)$에 대해서 $T$를 무한정 크게 늘린다면, 그것은 사실 비주기 함수와 같다고 이야기 하는 것이다
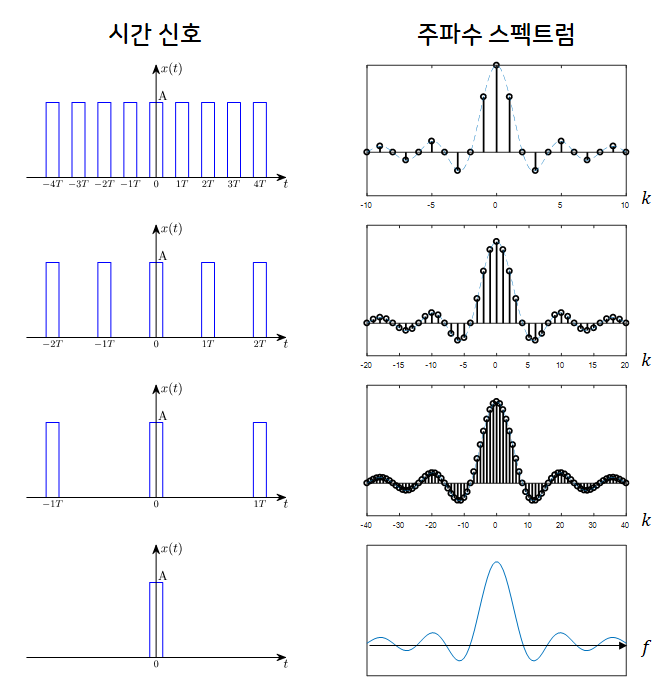
위 그림을 보게된다면, 이해가 쉬울 수 있다. (오른쪽 그래프들의 x 축은 k/T 즉, 주기의 역수인 주파수이기 때문에 각 주파수 영역에서 신호들의 강도를 나타낸 것이라고 할 수 있다.)
앞서 $c_k = \frac{1}{T}\int_{0}^{T}x(t)\exp\left(-j\frac{2\pi k t}{T}\right)dt$ 라고 정의된 $c_k$에서 주기 $T$가 무한정 길어지게 된다면, $c_k$ 의 주기가 계속해서 늘어나게 된다. (각$c_k$는 기저 주기 함수)
그렇게 된다면 이산화 정수인 $k$가 1,2,… 이렇게 증가한다고 할 때 주기가 무한정 늘어나게 되면 1과 2 사이의 간격이 상대적으로 더욱 좁아지게 될 것이다.
예를 들어 $\sin(2\pi x) $ 그래프와 $\sin(\frac{1}{4}\pi x)$ 그래프에서 0과 1 사이의 간격은 $\sin(2\pi x)$ 가 상대적으로 더 커지게 되는 것이다.
푸리에 급수에서 우리는 정수 k 를 뽑는데, 이 것을 일종의 Sampling 이라고 생각한다면 이 Sampling 간격이 매우 좁아져 결국에는 연속형 신호로 보이게 된다는 것이다.
즉, 다시말해 주기가 무한대인 일반적인 함수로 일반화 한다면, 표현 간격이 무한소로 작아지게 되기 때문에 주파수 스펙트럼이 연속 신호로 바뀌게 된다.
이러한 아이디어는 매우 강력하다고 할 수 있다. 자연에서의 어떤 신호는 여러 정현파들이 섞여있기 때문에 주기를 찾기가 어려울 수 있다.
하지만 그 신호를 비주기 함수로 취급하게 된다면, 푸리에 변환을 통해 해당 비주기 함수를 여러 주기 함수들로 Sampling 할 수 있게된다는 것이다.
DFS & DFT
이산 주기 함수의 경우 이산화 된 주기성의 성질에 의해 서로다른 주파수 성분이 $N$개를 넘을 수 없다.
이 의미는 우리가 분해할 주파수가 $N$개 이상일 수 없다는 것이다.
왜냐하면 기존 신호 $x(t)$ 의 주파수가 N = 10 이라면 연속형 데이터의 경우 0~10 까지 무한개의 k가 존재할 수 있지만, 이산화된 데이터의 경우 10개 이상으로 성분이 분해될 수 없기 때문이다.
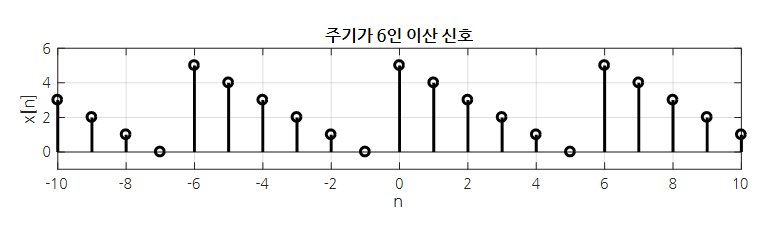
따라서 우리가 가진 신호 $x[t]$ 에서, 이산 시계열 데이터가 주기 $N$ 으로 반복한다고 할 때 DFT는 주파수와 진폭이 서로 다른 $N$개의 사인 함수의 합으로 표현이 가능하다.
여기서 연속형 데이터와 같이 주기 $N$ 을 무한대로 보낸다고 할 때 비주기 이산신호를 어떤 주기를 갖는 이산신호들의 집합으로 분해할 수 있게 되는데, 이 것을 DFT라고 하게 된다.

위 그림은 이산 신호를 이산 푸리에 변환을 진행한 것인데 DFT의 x축의 경우 주파수(주기의 역수)를 나타낸 것이다. 만약 이 신호에 Zero Padding 을 취하게 된다면, $x$ 축 $k/T$ 의 영역이 늘어나기 때문에 각 step인 k 의 거리가 상대적으로 좁아지므로 그래프가 더 촘촘하게 나타날 수 있다.
해당 그래프를 해석하는 방향은 각 $x$값의 주파수를 갖는 정현파들이 원 신호에서 얼마만큼의 영향력을 갖고 있는지로 판단할 수 있다.
따라서 그래프의 결과가 특정 함수 모양으로 나온다는 것은 여러 정현파들의 영향력이 특정 함수 모양을 따른다고 해석할 수 있다.
STFT

해당 그림은 스팩트럼과 스팩토그램에 대한 그림인데 보면 $x$축이 다르다.
왼쪽 그림의 경우 주파수에 대해 나타냈기 때문에 특정 시점에서의 신호를 여러 주파수의 정현파들로 분석한 그래프라고 할 수 있다.
대조되게 오른쪽 그래프의 경우 $x$축은 시간에 따른 그래프인데, 원 신호를 분해한 각 성분 신호들의 시간에 따른 변화를 나타낸 것이다.
대부분의 신호는 시간에 따라 주파수가 변하기 때문에 FFT의 경우 어느 시간대에 주파수가 변하는지, 즉 Time domain에 대한 정보가 사라지게 된다.
이러한 한계를 극복하기 위해 STFT 는 시간을 프레임별로 나눠서 FFT를 수행하게 하는 것이다. 즉, 짧은 시간에 스냅샷을 찍어 붙여 나열한 것이라고 할 수 있다.
시계열 데이터를 일정한 시간 구간(window size)로 나누고, 각 구간에 대해서 스펙트럼을 구하는 데이터이다. 따라서 Spectogram의 $y$ 축은 각 주파수를 갖는 신호들이 되는 것이며, $x$ 축은 Time domain, 색깔은 해당 시점에서 각 주파수의 신호가 얼마만큼의 세기를 갖고 있는지 나타내는 것이다.
- N : FFT size: Window 를 얼마나 많은 주파수 밴드로 나누는가(이산화 진행 시 주파수 개수 설정)
- $w(n)$ : window function : 일반적으로 hann window 사용(각 frame을 이어 붙여야 하기 때문에 frame 을 어떻게 잘라서 불연속성을 없애줄 것인지에 대한 것. 주로 양 끝단을 0으로 만드는 hann을 사용)
- n : window size : Window 함수에 들어가는 Sample 의 양이다.
- H : hop size : 윈도우가 겹치는 사이즈로 일반적으로 1/2 , 1/4 를 사용한다.
Time domain, Frequency domain
시간영역에서의 파형은 실제 종합된 파형 정보만을 나타낸다. 다시 말해 연속적인 신호에서 전체 시간에서 신호가 어떻게 흐르는지에 대한 지표라고 할 수 있다.
보통 보는 신호들은 시간 영역 즉, Time domain 에서 주기를 갖고 진동하는 것으로 나타낼 수 있다.
하지만 주파수 영역에서 다시 그리자면, Time domain이 아닌, 특정 신호가 어떤 주파수 영역의 세기들을 갖는지 나타내는 것이다.
예를 들어 한 신호를 30ms 로 잘라 해당 파형을 분석한다고 했을 때 시간에 대한 분석이 아닌, 주파수에 대한 분석을 진행하게 된다면, 어느 주기를 갖는 정현파가 얼마만큼의 세기로 섞여있는지 FFT를 통해 파악할 수 있는 것이다.