Source Filter Model
Source Filter Model
Introduction
Speech 의 생성 과정은 생각 -> 문장합성 -> 조음기관을 통해 발화 -> 공기를 통해 전파 -> 음성이 이해 식으로 진행된다
음성 생성의 경우 폐로부터 만들어진 공기가 성대를 통과하여 주기적인 신호를 갖는 공기의 흐름으로 바뀌며 이때 공기가 일정한 주파수를 갖고 떨린다면 이것을 Fundamental Frequency라고 부른다.
또한 성대에서 만들어진 신호나 노이즈와 같은 신호를 excitation 이라고 부르게 된다.
이렇게 생성된 공기의 흐름은 조음기관이 만든 공간(Cavity)를 지나게 되는데, 이 공간은 Oral cavity, Nasal cavity로 나뉜다.
- Excitation
- Voiced Sounds : 성대가 타이트하게 오픈이 됐을 때 주기성을 갖고 떨리게 된다. (풍선 구멍) 여기서 성대의 압력에 따라 Pitch가 바뀐다.
- Unvoiced sounds : 성대가 최대로 열려있을 때 주기적인 소리가 나지 않고 바람과 노이즈가 섞여 나온다.(빨대의 바람)
- Phones
- 모음(Vowel) : 공기 흐름의 저항이 없고 자음에 비해 지속된다.
- 자음(Consonant) : 입의 움직임이 매우 많고 공기의 저항이 많다.
Wave는 파동의 형태로 전달이 되는데, 주기란 패턴이 한번 반복될 때 걸리는 것이고 1초간 얼마나 진동하느냐가 주파수이다.
주파수가 높으면 공기를 쎄게 압축하는데, 이렇게 세게 압축할수록 Amplitude가 크고 소리가 세다
Sampling의 경우 Digital신호로 변화하는 것인데, 이 샘플링은 Time domain에서 수직축에 생성된다.
Quantization에서는 Sampling된 데이터가 Continous한 값을 갖고있기 때문에 이를 discrete한 값으로 변환시켜 주는 것인데, 수평축으로 범위를 나누는 것이라고 할 수 있다. (8-bit,16-bit)
Sampling 의 경우 나이키스트 이론에 따라 최대 주파수의 2배 이상을 Sampling rate를 가져가야 한다.
Why Frequency domain?
푸리에 변환에 가정하면 모든 복잡한 파형은 여러개의 sine wave의 합으로 이루어져 있음을 알 수 있다.
실제 복합파를 Time domain 영역에서 확인하게 되면 어떤 주기를 갖는 주파수가 얼마만큼 합성되어 있는지 파악하기 어렵기 때문에 이를 Frequency domain 에서 파악하게 된다. (여기서 Magnitude란 절댓값을 씌워 DB-scale로 나타낸 것)
DTFT
DTFT의 경우 시간 축을 $(-\infty , \infty)$ 로 설정한다. 이러한 무한의 영역은 값을 보기 불가능하며, 주파수 영역이 무한의 영역에서 연속적인 값을 갖는다고 설정하는 것은 실용적이지 않다.
따라서 유한한 시간 영역에서 신호를 이용하고 주파수 영역에서도 discrete한 신호를 갖는 것이 필요하다.
이러한 필요에 의해서 사용되는 것이 DFT이다. 이 것은 주파수 영역에서 Discrete한 값들만 사용될 때 선정 가능한 주파수는 N-1이기 때문에 유한한 영역에서 분석이 가능하다.
주로 FFT를 시행한다.
Spectrogram에서 주파수가 강한 영역은 Formant라고 부르게 되는데, 이 것은 조음기관으로 만들어진 공명주파수라고 한다.
이러한 Formant의 위치나 패턴을 통해 모음이나 자음들을 구분할 수 있다.
Source Filtering(음성 모델링)
- harmonics 란 기본적은 주파수가 있고 여러 배음들로 이루어진 주파수
Source Filtering 모델은 사람이 말을 하는 과정을 그대로 수학적으로 모델링하는 방식이다.
우선 인간의 소리 방식으로
- Vocal Fold(성대)는 진동을 하며 harmonics와 noise 를 만들게 되며, 주파수가 0인 신호의 Amplitude 가 가장 세며 고주파로 갈 수록 Amplitude 가 낮아진다.
- Vocal Tract는 성대에서 나온 Sound 가 조음기관을 통해 발음되는 즉, Filtering 되는 곳이다. 여기서 주파수 성분들이 얼마나 사용되는지 결정되며(DB) Transform이 된다.
- Output Spectrum 은 source spectrum이 filter function을 거쳐서 만들어 진다.
Source 모델이 Filter 를 거쳐 음성이 만들어진다.
Source
Source의 경우 주파수가 0인 신호가 fundamental Frequency이고 나머지가 하모닉스 배음이다.
여기서 Fundamental Frequency는 음의 높낮이를 나타내는 Pitch 와 Mel scaled 관계 즉, log 관계가 있다.
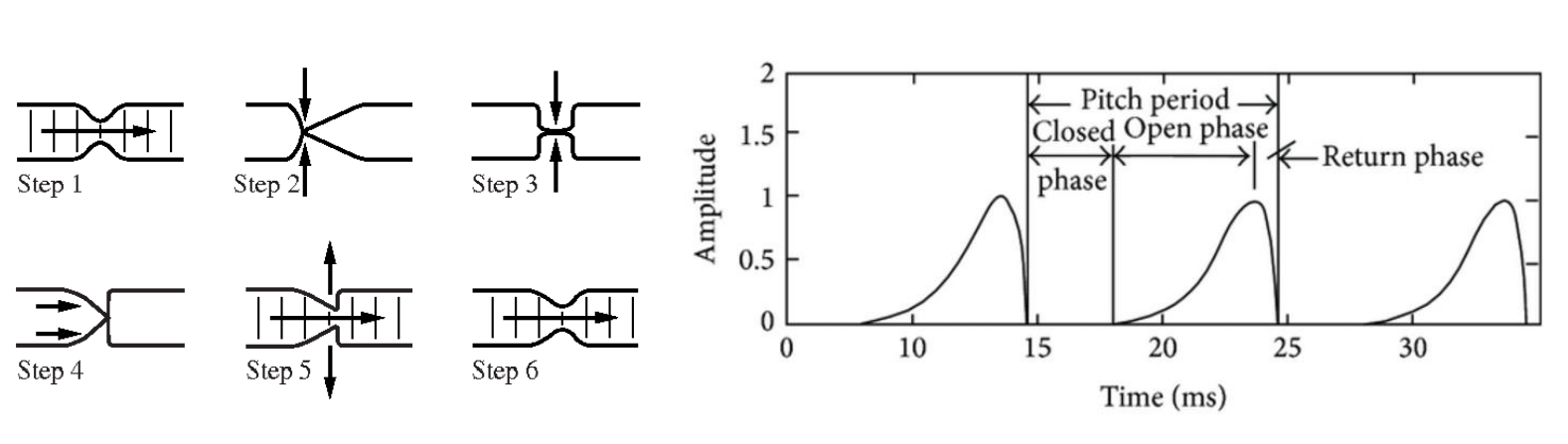
위 그림과 같은 Time domain 에서 Glottal wave가 있다고 할 때 한 wave의 주기를 $g[n]$ 이라고 한다면, 성대가 열리고 닫히는 성문운동의 전체 Glottal wave form 은 다음의 수식을 따른다.
- $u[n] = g[n] * p[n]$
- $g[n]$ : 한 주기의 glottal wave form
- $p[n] = \sum_{k=-\infty}^{\infty}\delta n -kP$ : impulse response
- $\tau = u[n,\tau] = w[n,\tau]$
여기서 $g[n] * p[n]$ 의 의미는 비주기 펄스 신호인 $p[n]$ 을 컨볼루션 해줌으로써 잘 알려지지않은 Glottal System 의 특성을 파악하고자 한 것이다.
Impulse의 수식을 살펴보면 델타 함수를 사용함을 알 수 있는데, 여기서 델타함수를 사용한 Impulse train 이란 특정 시점에서 값이 1 이 되는 함수이다.
이러한 델타함수를 Shift 하게 되준 것이 $\delta(n-kP)$ 가 되는데, 이 뜻은 P 만큼의 주기를 갖는 신호를 $kP$마다 활성화시켜 주는 것이다.
해당 함수를 Convolution 해주는 것은 입력된 신호에서 이산화 된 각 값 k 마다 활성화 되는 각 Impulse 신호를 Convolution 해주어 해당 함수를 Frequency Domain 에서 분해하여 표현하는 것을 가능하게 해준다.
또한 이러한 impulse response를 통해 glottal wave form 에서 해당 input 이 어떤 작용을 하는지 확인할 수 있다.
Filter
필터같은 경우 poles and zeros로 나타낼 수 있지만, 대개 all-pole 모델로 근사하게 된다.
Filter 는 튜브를 지나는 식으로 나타나는데 튜브의 형태에 따라 공진 주파수가 변하게 된다. (Formant)
Fundamental frequency의 경우 음의 높낮이를 결정하는 특성(Source)을 나타내며 formant의 경우는 어떠한 소리를 만들 것인가에 대해 영향을 준다.
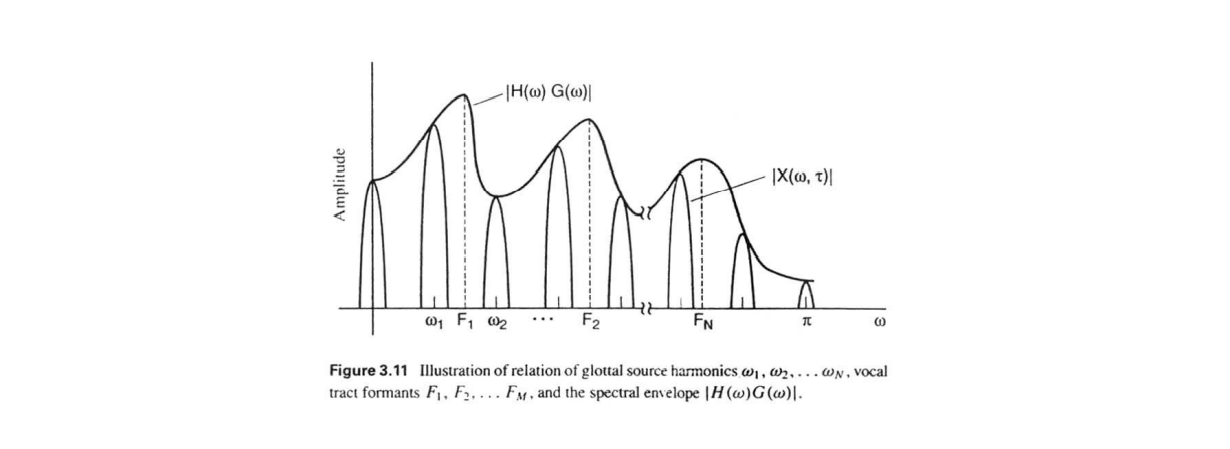
해당 그림은 Source로부터의 신호가 filter를 거치는 과정을 나타낸 것이다.
Frequency 영역에서 각 주파수의 성분 크기는 다음 그림의 높낮이가 다른 주기 함수꼴로 나타나져 있으며 envelop된 함수에서의 peek 는 원래의 Filter 의 Formant 로 볼 수 있다.
Source로 부터의 신호가 filter 를 거치는 과정은 수식적으로
- $u[n] = g[n]*p[n]$ : source로부터의 excitation
- $h[n]$ : vocal tract 의 impulse response
- $X[n] = h[n](g[n]p[n])$
- $\tau : x[n,\tau]$
로 나타난다.
기본적으로 Source와 같은 경우에는 Impulse train 이나 noise 로 모델링을 한다.
하지만 여기서 우리는 Vocal tract 에서 나온 $h[n]$ 을 추정해야 하며 이를 추정해야 Source-Filter modeling 이 수행된다.
따라서 우리는 Filter 를 추정해야 한다.
여기서 $h[n]$ (Impulse response)는 어떤 신호에서 활성화 되는 값들이라고 할 수 있다.
즉, 이것을 알면 Filter 함수를 알 수 있다.
위 그림상에서 봤을 때는 여러 함수를 Envelop 하고 있는 그래프를 추정하겠다는 의미라고 할 수 있다.
Linear Prediction
filter 는 uni-circle안에서 pole들로 생성된 값이라고 생각할 수 있으며 Zero와 같은 경우에는 입술, 비음과 관련된 묵음 신호이다.
Linear Prediction 에서는 Filter 를 All-pole 모델로 근사시키는데, 해당 과정을 통해 filter $H(z)$ 값을 추정한다.
- $H(z) = A/(1-\sum_{k=1}^P a_kz^-k)$
- $s[n]$을 추정하게 되면 filter $H(z)$를 추정할 수 있다.
- $s[n] = \sum_{k=1}^Pa_ks[n-k] + Au_g[n]$
- $s[n]$ : Discrete Time domain speech
- $u_g[n] $ : excitation
모델의 이산화 시간 영역에서 speech 의 계산은 앞선 시간의 speech 들의 선형 결합 꼴로 주어짐을 확인할 수 있다.
해당 과정에서 $s[n]$을 추정하는 방식으로 Mean Squared Error를 사용하는데, $P$란 얼마나 많은 시점의 과거 데이터를 불러와서 계산 할 것인지를 의미한다.
여기서 $s[n]$ 을 추정한다는 것은 Speech 즉, source-filter 의 결과물인 $s[n]$ 을 추정함으로써 중간 과정인 $H(z)$ 즉, Filter를 추정하게 된다.
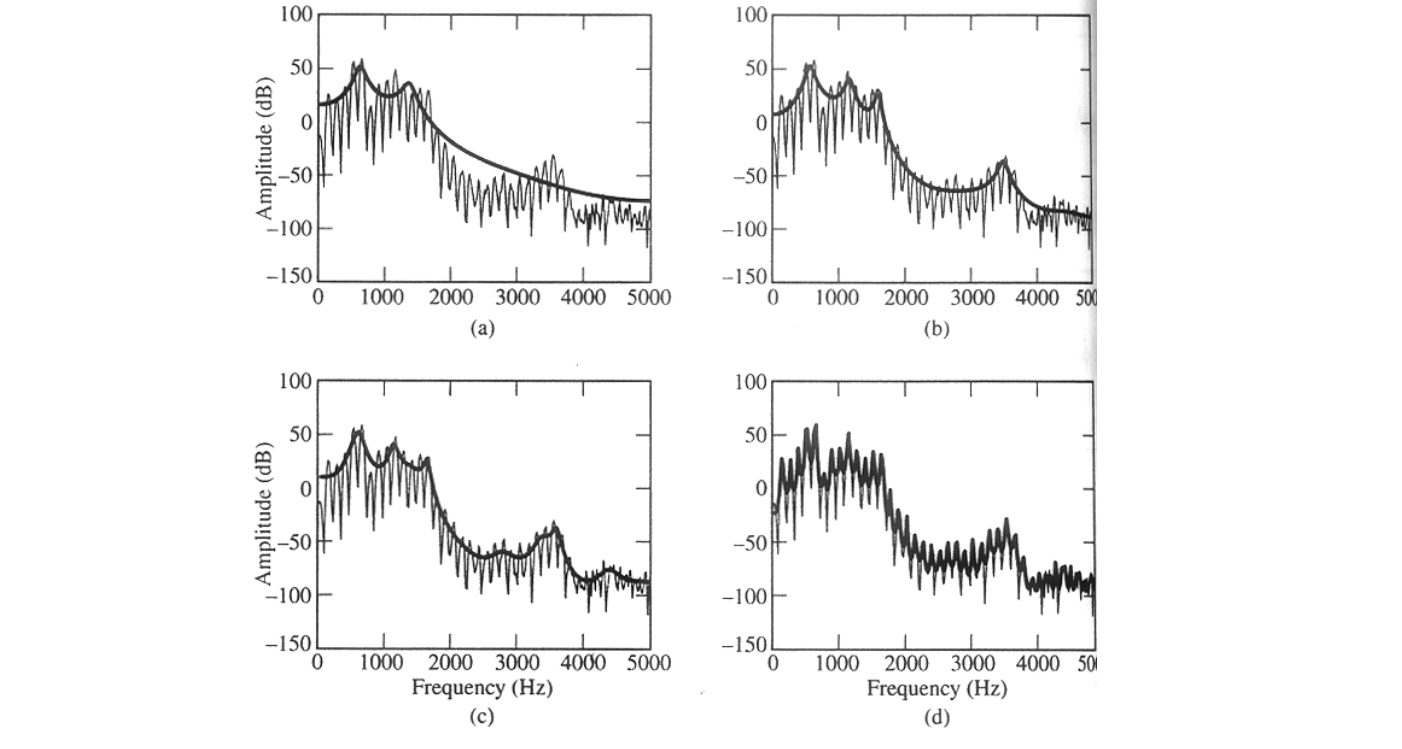
해당 그림은 과거 데이터 참조에 따른 vocal tract 의 envelop을 추정하는 것인데, LPC의 차수가 커질 수록 과적합이 많이 발생함을 확인할 수 있다.
Cepstrum Analysis
해당 방법은 filter 를 다른 방법으로 추정하는 것이다.
앞서 LP 같은 경우 all pole 모델을 가정함으로써 zero 인 비음, 입술음, noise등에 취약하다는 단점이 있었으나 Cepstrum analysis는 그런 가정이 없기 때문에 해당 문제로부터 자유롭다.

해당 그림은 Cepstrum Analysis를 나타낸 도식인데, 우선 $x[n]$을 이산화 푸리에 변환을 시킨 후 Log 를 취해 역 푸리에 변환을 실시하여 얻게 된다.