Markov Chain Monte Carlo Method
MCMC(Markov Chain Monte Carlo Method)
Introduction
앞선 서론에서 간단하게 얘기한 Sampling 에 대해서 이야기 해보겠다.
Beta 를 사전분포, Bernoulli 를 우도함수로 놓았을 때 두 함수의 곱으로 나올 수 있는 사후분포는 Beta 분포로 나오게 된다.
하지만 이러한 경우는 매우 특수한 경우이며 따로 켤레함수라는 이름으로 불리게 되는 여러가지 쌍이 있다.
그러나 실제 앞선 게시글의 문자데이터 예시처럼 가정해야하는 상황이 많고, 사전 분포를 설계할 때도 여러가지 고려사항이 많으며 사전 분포 자체도 여러가지 조건부 확률의 결합일 수 있다.
이렇게 된다면, 사후분포도 특정 방정식으로 표현되게 표현하기가 굉장히 어려워질 것이며, 아예 적분이 불가능한 함수로 결정되어 적분값을 구하지 못하는 경우가 생길 수도 있다.
따라서 이러한 난해한 함수들에 대해 샘플링을 적절하게 수행하여 우리가 원하는 사후분포에 비슷하게 추정될 수 있도록 하는 방법들을 알아보자.
Montecalro simulation
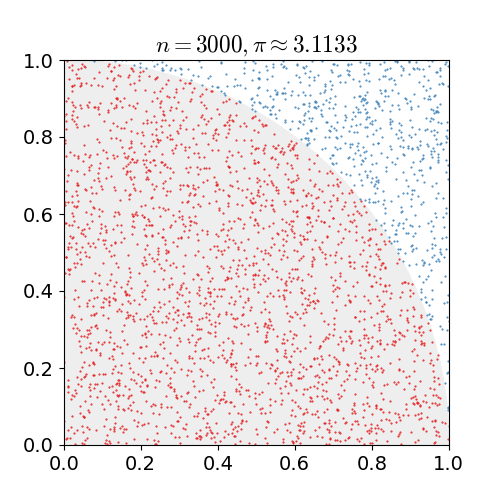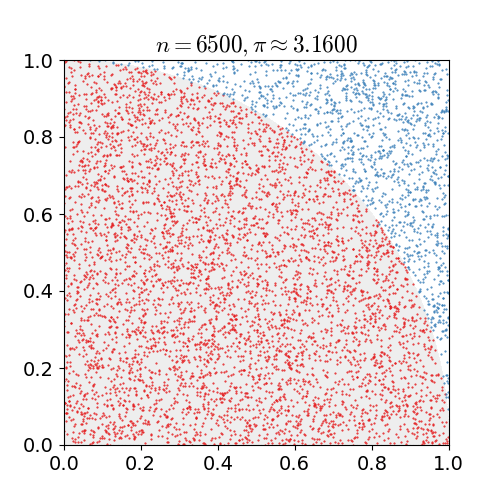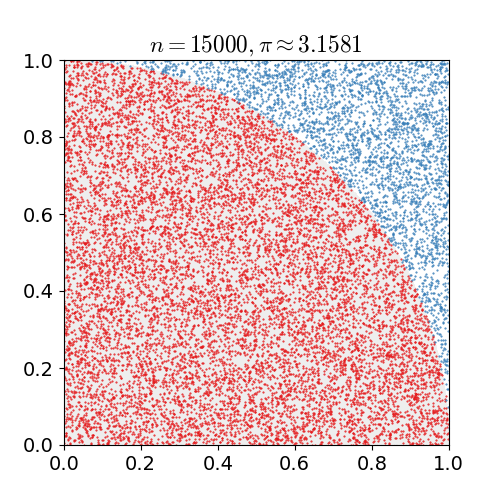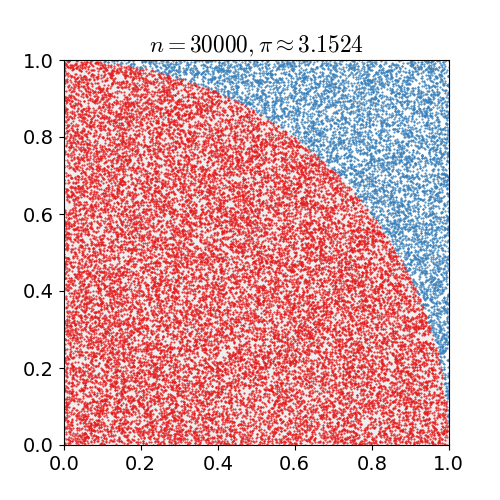
위 예시는 원주율 계산에 Montecarlo simulation 을 적용한 간단한 Example 이다.
Montecarlo simulation 이란 원주율과 같이 난해한 값들을 추정하기 위해 만들어진 것이다.
해당 방법론의 Idea 와 Flow는 다음과 같다.
- 한 변의 길이가 1인 정사각형에 원의 1/4을 꼭 맞게 그린다면 원의 넓이 공식에 따라 “사분원의 넓이: 정사각형의 넓이 = $\pi / 4:1$”임을 안다. 무리수 $\pi$가 어떤 값인지 모른다고 할 때 어떻게 $\pi$를 추정할 수 있을까?
- 정사각형 위에 일정 개수($n$)의 점을 균일하게 찍는다.
- $n$개의 점들 중 원의 사분면 안에 떨어지는 점의 개수($x$)를 센다. (즉, $x^2 + y^2<1$을 만족하는 점)
- $x/n \approx \pi/4$이므로 $\pi$를 $x/n\times 4$로 근사한다.
이렇게 n 을 계속해서 늘리며, 점의 개수를 근사시킨다면 $\pi$ 값과 비슷한 결과를 얻을 수 있음을 확인할 수 있다.
이러한 방법론을 확률 분포에 대해서 설정해보자.
- $X$가 $N(0,1)$을 따르는 정규분포라고 하자. $e^x$의 기대값은 무엇인가?
- 수리통계 식 해결: 정규분포의 Fomula 는 우리가 직접 확인할 수 있으므로 정규 분포의 식을 아래와 같이 적분하면 됨
- \[\int_{-\infty}^{\infty} e^x \cdot \frac 1{\sqrt{2\pi}} e^{-\frac {x^2} 2} dx\]
그러나 Monte Carlo Simulation 방법을 차용한다면 다음 계산은 단순 샘플링 작업에 불과한다.
우리는 정규분포의 pdf 를 알고있기 때문에 정규분포의 pdf 에서 엄청나게 많은 샘플링을 진행한 이후 해당 값의 평균을 내주면 정규분포의 평균을 구할 수 있다.
# pymc3 사용
import pymc3 as pm
import numpy as np
with pm.Model() as model:
x = pm.Normal('x', 0, 1)
위와같이 Sampling을 진행한 후 해당 x 값을 승수로 곱해주어 평균을 내어주면 앞서 정통적인 방식으로 구한 적분 값과 매우 근사한 결과를 나을 수 있을 것이다.
여기서 헷갈리면 안되는 점이 있다.
Monte Carlo Simulation은 단순히 Sampling을 하면 근사치가 나올 것이다. 라는 아이디어 정도로만 생각해야 한다는 것이다.
정규분포에서 Sampling 을 하는 것이 MonteCarlo Simulation이 아니라, Sampling 을 하면 근사치가 나올 것이다라는 결과에 대한 Idea 가 Monte Carlo Simulation인 것이다.
따라서 정규분포에서 어떻게 Sampling 을 하는지에 대한 것은 아예 다른 이야기일 수 있다.
Sampling의 경우 매우 어려운 작업이 될 수 있다.
Sampling이란, 해당 분포에서 어떤 값을 추출하는 행위인데, Sampling이란 단어에 우리가 익숙해서인지 굉장히 간단한 것 같지만 실제로 어떤 함수 $P(x)$ 에서 10000번 Sampling을 진행한다고 했을 때 $P(x)$ 의 Pdf 모양과 비슷하게 Sampling 값들의 분포가 형성되기 위해서 우리가 해야할 일은 조금 복잡하다.
단순하게 정규분포에서 샘플링을 해본다고 생각해보자.
$P(x)$ 가 정규분포를 따르는 함수라고 할 때 우리는 $x$ 에 어느 값을 집어넣으며 Sampling을 해야 정규분포에 근사한 결과를 낼 수 있는가?
생각보다 어려운 질문일 것이다. 정규분포의 경우 연속확률분포이기 때문에 단일 Scalar 값에 대한 확률 값을 추출할 수 없다.
정확하진 않지만 $P(0)$ 을 넣어서 나오는 값 만큼의 비율을 0에서 추출하고, $P(0.5)$ 만큼 넣어서 추출하고 하는 식으로 진행할 수 있겠지만 취지는 생각보다 샘플링을 어떻게 하는지가 깨나 복잡할 수 있다는 것이다.
물론 정규분포의 경우 Sampling을 하는 방식은 CDF 를 구한 후 해당 CDF 의 Inverse 에 값을 대입하여 진행한다.
따라서 우리는 Sampling 을 어떻게 진행해야 복잡한 분포의 모양에 맞는 결과를 기대할 수 있는지에 대해 고민해보아야 한다.
여기서 복잡한 분포란, 역함수를 구하는 과정이 복잡할 수도 있으며, 적분 자체가 불가능한 함수들 일 수도 있다.(Ex: Logistic 역함수)
즉, Monte Carlo Simulation의 Idea 로 Sampling을 진행하는 것이 직접 값을 계산하는 것보다 쉬운 것임을 알았는데, Sampling을 어떻게 하는가에 대한 질문이 남아있다.
컴퓨터에서의 Sampling
이부분은 개인적으로 Sampling을 이해하기 위해 좀 더 파본 이야기이다.
PDF 와 CDF 는 확률밀도함수, 누적확률 분포이다.
CDF 의 경우 $CDF(x)$ 의 값으로 나오는 것이 해당 값 까지의 총 확률이다.
따라서 대응되는 $CDF(x) = y$ 는 거기까지의 확률이 되는데, 만약 여기서 우리가 $CDF^{-1}(y)$ 라는 식을 계산하게 된다면, 어떤 특정 확률을 넣었을 때의 지점이 나오게 되는 것이다.

굉장히 화질이 깨지지만 위 그림은 표준 정규분포의 CDF 이다.
여기서의 $F(X)$ 가 특정 지점에서의 누적 확률을 나타내게 된다.
우리가 만약 $Uniform(0,1)$ 에서 무작위로 값을 추출하여 $CDF^{-1}$ 함수에 집어넣게 된다면, 특정 지점이 나오게 될 것이다.
그 함수가 만약 $y=x$ 함수라면, Sampling 결과는 Uniform Distribution의 PDF 와 비슷한 모양을 띄게 될 것이다. 하지만 위와 같은 표준 정규 분포의 $CDF$ 의 역함수를 따라 Sampling 을 진행하게 되면 결과적으로 우리는 특정 지점들에 대해 Sampling 할 수 있으며, -1~1에서 함수값의 차이가 많이 없기 때문에 당연히 -1~1쪽으로 Samlpling 결과가 집중되게 될 것이며 정규분포 PDF와 비슷한 형태로 Sampling이 가능해질 것이다.
Rejection Sampling
Sampling을 하는 알고리즘인 Rejection Sampling에 대해 결론부터 말하면 다음과 같은 알고리즘이다.
- $q(x)$에서 $x_0$를 생성한다.
- Uniform(0,1)에서 $u$를 생성한다.
- 만일 $u\leq \frac{p(x_0)}{Mq(x_0)}$이면 y를 샘플로 채택, 만일 조건을 만족하지 못하면 기각한다. ($y$ 는 $q(x_0)$ 의 샘플링 결과)
- $\frac{p(y)}{Mq(y)}$ 가 1과 가깝다면 A,B 거리가 상대적으로 작은 것이라고 할 수 있으며, unniform 하게 뽑은 $\mu$ 값은 해당 비율보다 작을 확률이 매우 클 것. 따라서 두 값의 차이가 작다면 대부분의 가설은 채택을 한다는 뜻이다.
풀어서 설명하자면 다음과 같다.
- 우리는 $p(x)$ 에 대해 추정하고 싶다.(매우매우 어려운 분포)
- $p(x)$를 감쌀 수 있는 $q(x)$ 분포를 만들자.(상대적으로 샘플링이 가능한 분포)
- $\frac{p(x_0)}{Mq(x_0)}$가 1보다 매우 작다는 것은 $A$길이가 $B$보다 상대적으로 매우 크다는 것. 따라서 너무 크게 감쌌기 때문에 $p(x)$분포를 정확하게 추정하기 어려울 것
- 반대로 1인 것은 $A$ 의 길이가 거의 0이 된다는 것으로 상대적으로 잘 감쌋다는 것
- 만약 1과 비슷하다면 $u$ 의 값이 대체적으로 더 작을 것이기 때문에 샘플로 취할 가능성이 매우 높다.
- 따라서 해당 지역에서는 샘플이 많이 추출될 것
따라서 의미는, $p(x)$ 분포를 감싸는 $q(x)$ 분포가 $p(x)$ 를 상대적으로 잘 감쌋는지에 대한 것으로 표현할 수 있을 것이다.
해당 알고리즘의 기본 아이디어를 차용하여 MCMC 와 해당 개념을 통한 대표적인 샘플링 기법인 MH 에 대해 알아보자.
Markov chain Monte Calro
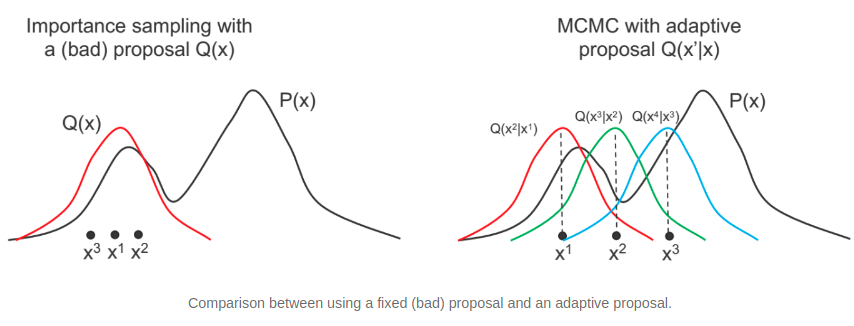
위의 그림은 MCMC의 아이디어를 잘 표현한 그림이다.
위의 그림에서 대략적으로 표현된 것처럼 $i$번째 샘플을 참고하여 $i+1$ 번째 샘플을 추출하는 것이 MCMC의 아이디어라고 할 수 있는데, Markov chain 이란 이름은 $i$ step 의 값이 $i+1$ 번째 값에 영향을 주기 때문에 붙인 이름이라고 해석할 수 있다.
| 한 문장으로 표현하자면 여러 상태(state) $x_1, x_2, …$가 주어져 있고 $x_i$에서 $x_j$로 이동할 조건부 확률 transition distribution $T(x_j | x_i)$이 주어져 있어 매 step마다 이 확률값에 따라 이동하는 확률과정이라고 할 수 있다. |
예를 들어 $x_1$ 이 샘플링 되었다고 할 때 $x_1$ 에서 임의의 분포를 만들어 $x_2$ 를 추출하고 동일한 방법으로 $x_3$ 을 추출하는 방식으로 앞서 이야기한 Rejection Sampling 의 아이디어가 녹아든 것이라고 할 수 있다.
이 방법을 통해 Sampling 을 진행하는 방식인 Metropolis Hasting’s method 에 대해 좀 더 살펴보자.
Metropolis Hasting’s method(M-H method)
MH 의 알고리즘은 다음 과정으로 표현될 수 있다.
- 특정 현재 위치에서 시작한다.
- 현재 위치 주변에서 새로 이동할 위치를 조사한다. (주변의 조약돌을 조사)
- 데이터와 사전확률분포에 따라 새로운 위치를 수용할지 안할지 판단한다. (새로운 조약돌이 그 산에서 나올 가능성을 조사)
- (a) 수용한다면 새로운 위치로 이동하고 1단계로 이동한다. (새로운 조약돌을 취함) (b) 수용하지 않는다면 기존 위치에서 1단계로 이동한다. (새로운 조약돌을 무시)
- 수많은 반복 후에 모든 가능성 위치를 돌려준다. (모든 조약돌의 위치를 모음)
위 과정은 눈을 감은채로 산을 내려갈 때와 비슷한 상황이라고 할 수 있다.
여러 방향으로 한발자국씩 내딛을 때, 해당 방향이 내려가는 방향이라면 한 발자국을 내딛고, 아니라면 다시 원상태로 돌아와서 다른 방향으로 발을 내딛는 과정이라고 생각하면 된다.
여기서 내가 가는 방향을 360가지라고 가정한다면, 우리가 갔던 방향을 Counting 하게 된다면, 내가 원래 있던 방향에서 발을 내딛을 방향의 확률분포에 근사한 샘플링 결과가 생길 수 있다.
조금 더 수학적으로 이야기 하자면 다음과 같다.
- Target distribution: $\pi(x)$ 일반적으로 사후 분포
- Proposal distribution: $ N(x^{(t)}, \sigma^2)$ x 를 어디서 뽑을지 정함
- 초기값 $x^{(0)}$을 결정한다.
- $t=0, 1, …$에 대하여 다음의 과정을 반복 수행한다.
- $y$를 random walk 방법으로 발생시킨다.
- $y=x^{(t)}+\epsilon, ~~\epsilon\sim N(0,\sigma^2)$
- $u$를 균일분포 $U(0,1)$로부터 발생하여, 다음의 과정을 수행한다.
\(x^{(t+1)} = \left\{ \begin{matrix}
y,& \mbox{if }u<\alpha(x^{(t)}, y)\\
x^{(t)}, & \mbox{otherwise}
\end{matrix}\right.\)
\(\alpha(x, y) = \min \left\{ 1, \frac{\pi(y) }{\pi(x)} \right\}: \mbox{Acceptance Probability}\)
- 많이 작다는 것의 의미는 많이 떨어져있는 Sample 이라는 뜻이기에 $\mu$ 값에 따른 샘플 뽑기 확률도 낮아지게 설정한다.
- $\frac{\pi(y) }{\pi(x)}$ 가 1을 넘는다는 의미는 전 스텝의 x 보다 다음 스텝의 샘플이 나올 확률이 더 크다고 판단하는 것이므로 무조건 샘플링
- $y$를 random walk 방법으로 발생시킨다.
여기서 $y$ 는 $\epsilon$ 만큼의 Noise 를 갖고있는 표준정규분포의 형태로써, $\frac{\pi(y) }{\pi(x)}$ 의 경우 작으면 작을수록 기존 $x$ 값을 Input 으로 넣었던 사후 분포의 값이 더 크다는 것이기 때문에 샘플링을 그만큼 적게 가져간다.
물론 $u$ 는 0이 될 수도 있기 때문에 아예 샘플링을 하지 않는다는 뜻은 아니지만, $\frac{\pi(y) }{\pi(x)}$가 큰 다른 경우보다 확실히 적게 샘플링이 될 것이다.
우리는 사후 분포가 어떤 형태를 띄고있는지 잘 알 수 없지만 위와 같은 과정을 반복하다보면 상대적으로 확률이 큰 $x_a$ 지점에서는 많이 샘플링이 될 것이다.
그 이유는 $\alpha(x,y)$ 값이 작을 것이기 때문이다.(주변 다른 $x_i$ 지점보다 확률이 크므로 $\frac{\pi(x_i) }{\pi(x_a)}$ 값은 작고 따라서 샘플링이 더 적게 이뤄질 것이다.) 또 반대로 $x_a$ 가 상대적으로 확률이 적은 지점이라면 random walk 를 진행할 때 상대적으로 sampling 이 잘 되지 않을 것이다.(물론 0으로 수렴한다 하더라도 $u$ 값이 0일 수도 있기 때문에 샘플링이 아예 안되는 것도 아니다.)
여기서 만약 움직이는 보폭인 $\epsilon$ 이 크다면 그만큼 탐색의 영역도 커지게 될 것이고 이렇게 된다면 제대로 된 샘플링이 이뤄지지 않을 것이다.
따라서 $\epsilon$ 을 잘 설정하는 것이 관건이라고 할 수 있다.
Result
현재 너무 많은 개념을 이야기했기 때문에 각 개념들의 포함관계가 불분명해 질 수 있다.
잘 생각해보면 이 M-H 알고리즘은 앞에서 이야기한 MonteCarlo Simulation 의 아이디어가 녹아져있다.
